CoCalc Blog
Hal Snyder • • cocalc and python
Create interactive data visualizations for collaborators in your CoCalc projects using Dash.
Dash is an open-source framework to create web applications with Python. With CoCalc’s Run A Webserver capability, you can run a Dash application from inside a CoCalc project.
William Stein • •
Nearly 3 years ago, I gave a talk at a Harvard mathematics conference announcing that “I am leaving academia to build a company”. What I really did is go on unpaid leave for three years from my tenured Full Professor position. No further extensions of that leave is possible, so I finally have to decide whether or not to go back to academia or resign.
Nearly two decades ago, as a recently minted Berkeley math Ph.D., I was hired as a non-tenure-track faculty member in the mathematics department at Harvard. I spent five years at Harvard, then I applied for jobs, and accepted a tenured Associate Professor position in the mathematics department at UC San Diego. The mathematics community was very supportive of my number theory research; I skipped tenure track, and landed a tier-1 tenured position by the time I was 30 years old. In 2006, I moved from UCSD to a tenured Associate Professor position at the University of Washington (UW) mathematics department, primarily because my wife was a graduate student there, UW has strong research in number theory and algebraic geometry, and they have a good culture supporting undergraduate research.
Before I left Harvard, I started the SageMath open source software project, initially with the longterm goal of creating a free open source viable alternative to Mathematica, Maple, Matlab and Magma. As a result, in addition to publishing dozens of research mathematics papers and some books, I also started spending a lot of my time writing software, and organizing Sage Days workshops.
At UW, I recruited an amazing team of undergraduates and grad students who had a major impact on the development of Sage. I was blown away by the quality of the students (both undergrad and grad) that I was able to get involved in Sage development. I fully expected that in the next few years I would have the resources to hire some of these students to work fulltime on Sage. They had written the first versions of much of the core functionality of Sage (e.g., graph theory, symbolic calculus, matrices, and much more).
I was surprised when my application for Full Professor at UW was delayed for one year because – I was told – I wasn’t publishing enough research papers. This was because I was working very hard on building Sage, which was going extremely well at the time. I took the feedback seriously, and put more time into traditional research and publishing; this was the first time in my life that I did research mathematics for reasons other than just because I loved doing it.
I tried very hard to hire Bill Hart as a tenure-track faculty member at UW. However, I was told that his publication count was “a bit light”, and I did not succeed at hiring him. If you printed out the source code of software he has written, it would be a tall stack of paper. In any case, I totally failed at the politics needed to make his case and was left dispirited, realizing my personal shortcomings at department politics meant I probably could not hire the sort of colleagues I desperately needed.
UW was also very supportive of me teaching an undergrad course on open source math software (it evolved into this). I taught a similar course at the graduate level once, and it went extremely well, and was in my mind the best course I ever taught at UW. I was extremely surprised when my application to teach that grad course again was denied, and I was told that grad students should just go to my undergraduate course. I thought, “this is really strange”, instead of lobbying to teach the course and better presenting my case.
To be clear, I do not mean to criticize the mathematics department. The UW math department has thought very hard and systematically about their priorities and how they fit into UW. They are a traditional pure mathematics departments that is generally ranked around 25 in the country, with a particular set of strengths. There is a separate applied math department on campus, several stats departments, and a massive School of Computer Science. Maybe I was in the wrong place to try to hire somebody whose main qualification is being world class at writing mathematical software. This blog post is about the question of whether the UW math department is the right place for me or not.
My number theory research received incredible support from the NSF, with me being the PI on six NSF grants. Also, Magma (which is similar to Sage, but closed source) had managed to find sufficient government funding, so I remained optimistic. Maybe I could fund people to build Sage via grants, and even start an institute! I applied for grants to support work on SageMath at a larger scale, and had some initial success (half of a postdoc, and some workshops, etc.).
Why is grant funding so important for Sage? The goal of the SageMath project is to create free open source software that is a viable alternative to Mathematica, Maple, Matlab, and Magma – software produced by companies with a combined thousands of fulltime employees. Though initial progress was encouraging, it was clear that I desperately needed significant money to genuinely compete. For example, one Sage developer had a fantastic Sage development project he wanted about 20K to work fulltime on during a summer, and I could not find the money; as a result he quit working on Sage. This project involved implementing some deep algorithms that are needed to more directly compete with Mathematica for solving symbolic inequalities. This sort of thing happened over and over again, and it began to really frustrate me. I could get plenty of funding for 1-week workshops (just travel expenses – everybody works for free), but there’s only so much you can do at such sprints.
I kept hearing that there would be a big one-in-10-years NSF institutes competition sometime in the “next year or two”. People hinted to me that this would be a good thing to watch out for, and I dreamed that I could found such an institute, with the mission to make it so the mathematics community finally owned the deep software on which teaching and research are based. This institute would bring the same openness and robustness to computational mathematics that rigorous proof had brought to mathematics itself a century earlier.
Alas, this did not happen. I remember the moment I found out about the actual NSF institutes competition. Joe Silverman was standing behind me at a coffee break at The Arizona Winter School 2010 telling people about how his proposal for ICERM had just won the NSF institutes competition. I spun around and congratulated him as I listened to how much work it was to put together the application during the last year; internally, my heart sunk. Not only did I not win, I didn’t even know the competition had happened! I guess I was too busy working on Sage. In any case, my fantasy of creating an NSF-funded institute died at that moment. Of course, ICERM has turned out to be a fantastic institute, and it has hosted several workshops that support the development of open source math software.
Around this time, I also started having my grant proposals denied for reasons I do not understand. This was confusing to me, after having received so many NSF grants before. In 2012, the Simons Foundation put out a call for something that potentially addressed what I had hoped to accomplish via an NSF-funded institute. I was very excited again, but that did not turn out as I had hoped. So next I tried something I never thought I would ever do in a million years…
William Stein • • cocalc
CoCalc is a web application that lets you collaboratively use a large amount of free open source math and data related open source software. You can create collaborative Jupyter notebooks, edit LaTeX documents, use Terminals, use graphical Linux applications, create chatrooms, and much more. There’s extensive support for SageMath, Octave (a MATLAB clone), and R. See the docs.
Cocalc-docker is a completely free and open source self contained version of CoCalc, which you can run on your own computer or cloud server. This post is about how to freely play around with running CoCalc-docker on Google Cloud Platform.
If you scroll down and see all the cool things CoCalc can do, but don’t want to bother running your own server, make an account at CoCalc and use our hosted service, which has filesystem snapshots, a vast amount of preinstalled software (much more than cocalc-docker), and support.
Choose a location near you:
Click the checkbox next to “Deploy a container image to this VM instance.”, then
put sagemathinc/cocalc in the blank below “Container image”. Also check
the boxes next to buffer stdin and allocate a tty.
You can also change the machine type, though the default will work.
http://www.sagemath.org/
If you are just playing around to test this out, open “Management, security, disks, networking, sole tenancy” and scroll down and set “Preemptibility” to On. This will make things way cheaper (using less of your free trial credits). This is especially useful if you wan to do a relatively quick but very CPU intensive parallel computation.
Here’s how our cost estimate comes out so far, with preemptible on. It would be about four times as expensive without preemptible on.
Of course the drawback of preemptible is that the machine will be killed within 24 hours. That’s fine for testing things out though.
Once the VM is created, click to open it, then click “Serial port 1 (console)” (or “Connect to serial console”), to watch the log as the machine boots up.
It takes at least 10 minutes to pull and decompress the sagemathinc/cocalc Docker image. If this fails, you
probably forgot to increase the size of the boot disk from 10GB to 20GB (or more), in which case you should delete everything
and start over.
Once your machine is running and the sagemathinc/cocalc image has been pulled and decompressed,
find the external ip address of your machine, and open it in a new browser tab. In my case, I
open https://35.227.184.91/.
Do NOT choose the address that starts 10., since that is internal.
If this fails, you probably forgot to check the box next to “Allow HTTPS traffic”.
Since the SSL cert in the Docker image is self-signed, you’ll get a warning. Click through it by clicking “ADVANCED”.
WARNING: Anybody who knows the IP address can make an account in the same way. There’s no secret token, and currenly no way to configure one with GCP Container Image. See this issue.
William Stein and Hal Snyder • • cocalc
The goal of CoCalc is to make all open source mathematics and data science software easily available in your web browser, in order to reduce the barriers to using open source software for teaching courses and doing research. For many years, people have been requesting the ability to run standard graphical Linux applications in CoCalc. Until now, we have primarily focused on Jupyter notebooks, and other “native” web applications. However, we finally figured out how to bring standard graphical Linux applications to CoCalc, which will further help in our mission of removing barriers to using free open source software in teaching and research.
CoCalc now has X11 graphical support, which lets you run any graphical Linux application in your browser. You want to try this out: Go to CoCalc.com, make an account, create a project, then click
+New and select X11 Desktop.
You’ll get an xterm.js terminal on the left and a blank desktop on the right.
Type xclock&
in the terminal then press enter, and you’ll see a tab appear on the right. Click it and
see a clock.
Type python3 in the terminal, and try something involving
Turtle graphics, and it will just work:
•
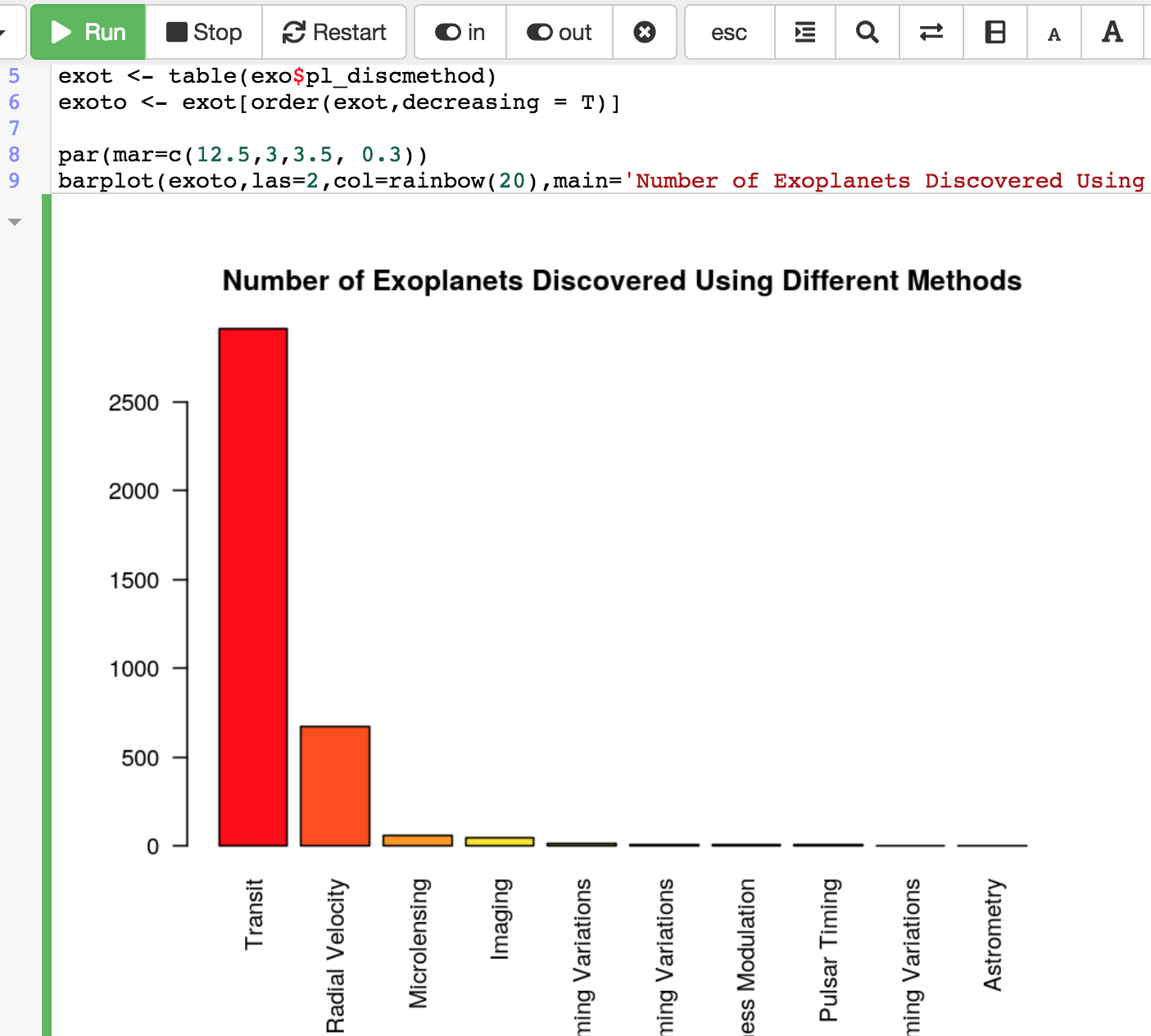
This paper about collaborative editing is on Hacker News today. I also recently talked with Chris Colbert about his new plans to use a CRDT approach to collaborative editing of Jupyter notebooks. This has caused me to be very curious again about how CoCalc’s collaborative editing is related to the many algorithms and research around the problem in the literature.
Protocols for collaborative editing are a venerable problem in computer science, and there are probably over a hundred published research papers on it. The basic setup, going back three decades, is that sync algorithms are supposed to have three properties, which I’ve stated in simplified plain language below:
CoCalc has 1, of course; without that you’ve got nothing.
CoCalc has 2, when people’s clocks are synced, because all patches you’ve applied have timestamp less than now (=time when making the patch).
CoCalc does NOT have 3, for some meaning of 3. Patches are applied on a “best effort basis”. So instead of our changes being “insert the word ‘foo’ at position 7”, they are more vague, e.g., apply this patch with this context using these parameters to determine Levenshtein distance between strings. With intention preservation, if the operation is “insert word ‘foo’ at position 7”, definitely that’s exactly what happens whenever anybody does it (‘foo’ will appear in the document) – it does not depend at all on context. With diffmatchpatch patches (which we use in CoCalc), the effect of the patch depends very much on the document you’re applying the patch to. If there is insufficient context, then ‘foo’ might not get inserted at all.
Similar remark apply to how I designed the structured object sync in CoCalc, which is used, e.g., for CoCalc Jupyter Notebooks; it also applies patches on a best effort basis.
This is a protocol that in theory has all of 1-3. Of course there are many, many specific versions of OT. The hard part is ensuring 3, and it can be complicated. The problem to be solved makes sense, and it can be done. The details (and implementing them) are certainly nontrivial to think about conceptually… There’s many academic research papers on OT, and it’s implemented (well) in many production systems.
In OT, the data structure that defines the document is simple (e.g., just a text string), and the operations are simple, but applying them in a meaningful way is very hard. This paper on HN that I mentioned above argues that OT is much more popular in production systems than CRDT.
This also does 1-3. It sets everything up so the data structure that defines the document is very complicated (and verbose), but it’s always possible to merge documents in a consistent way. What is difficult gets pushed to different places in the protocol than OT, but it’s still quite hard, and there are subtle issues involved with any non-toy implementation.
CoCalc’s text editing does synchronization as follows. Each user periodically computes a timestamped patch, then broadcasts it to everybody else editing the same file. When patches arrive, each user computes the current state of the document as the result of applying all patches in timestamp order. If everybody stops editing, then they all agree on the same document.
This protocol satisfies 1 and 2, but not 3. The reason is that patches are applied on a best-effort basis using the diff-match-patch algorithm. For example, a patch made from deleting a single letter in a document can, when applied to a different document end up deleting multiple letters (or none). Basically, CoCalc replaces all the very hard work needed for 3 that OT and CRDT’s have with a notion of applying patches on a “best effort” basis. The behavior is well defined (because of the timestamps), but may be surprising when multiple people do simultaneous nearby edits in a document.
The paper says:
“There are two basic ways to propagate local edits: one is to propagate the edits as operations [12,38,50,51,73]; the other is to propagate the edits as states [13]. Most real-time co-editors, including those based on OT and CRDT, have adopted the operation approach for propagation for communication efficiency, among others. The operation approach is assumed for all editors discussed in the rest of this paper”.
Here [13] is N. Fraser’s paper on Differential Sync. This was the sync algorithm in the first version of CoCalc, and was the inspiration for what CoCalc currently does.
In CoCalc, the data structure that defines the document is simple (just a text string, say), and the operations are less simple (computing diffs, defining patches), and applying them in a meaningful way is somewhat difficult (it’s what the diffmatchpatch library does). This approach is very easy to think about and generalize, since it is self contained and a local problem. After all, I mostly described the algorithm in a single paragraph above!
In CoCalc, we compute diffs of arbitrary documents periodically, much like how React.js DOM updates work. This seems to not be needed in OT or CRDT, which instead track the actual operations performed by users (i.e., type a character, delete something). Computing diffs has bad complexity in general, but very good complexity in many cases that matter in practice (that’s the trick behind React). Diffs involve observing state periodically, rather than tracking changes.
OT and CRDT really are solving a much harder problem than we solve. This is similar to how git uses the trick of “assume sha1 hashes don’t collide” to solve a much easier problem than the much harder problems other revision control systems like Darcs solve.
There is a nice example to illustrate how CoCalc fails for this third “user intention” requirement. This is called “the TP2 puzzle”. You can try the following in both CoCalc and Overleaf (which probably does some OT algorithm):
I do NOT consider this a bug in CoCalc – it’s doing exactly what is implemented, and what I as the author of the realtime sync system intended. The issue is that the patch to delete “b” has “a” and “cd” as surrounding context, and if you look at how diffmatchpatch patch application works, this is a case where it just deletes everything inside the context.
Evidently, Google Wave also had issues with TP2 because fully implementing OT is…
“… hard! In fact, almost all published algorithms that claim to satisfy TP2 have been shown to be flawed.”
The “famous” TP2 puzzle for CoCalc ends up like this (in at least 1 of the 6 possibilities!).
Start with
abc
then add an x and a y on either side of b, and delete b.
In one order, end up with
acxd
The patches are:
[[[[0,"--\n\n\nabc"],[1,"x"],[0,"d\n\n\n\n\n"]],5291,5291,14,15]]
[[[[0,"---\n\n\nab"],[1,"y"],[0,"cd\n\n\n\n\n"]],5290,5290,15,16]]
[[[[0,"\n---\n\n\na"],[-1,"b"],[0,"cd\n\n\n\n\n"]],5289,5289,16,15]]
Applying the “delete b” patch, also deletes the y:
apply_patch([[[[0,"abc"],[1,"x"],[0,"d"]],5291,5291,14,15]], 'abcd')
(2) ["abcxd", true]
apply_patch([[[[0,"ab"],[1,"y"],[0,"cd"]],5290,5290,15,16]], "abcxd")
(2) ["abycxd", true]
apply_patch([[[[0,"a"],[-1,"b"],[0,"cd"]],5289,5289,16,15]], "abycxd")
(2) ["acxd", true]
Looking at the source code of diffmatchpatch, this is just what DMP does. If there is a lot more badness and the strings are bigger, it’ll refuse to delete. It really is a sort of “best effort application of patches” with parameters and heuristics; no magic there.
William Stein and Hal Snyder • • cocalc
Prior to CoCalc, William Stein spent 15 years teaching and doing research using mathematical software at Berkeley, Harvard, UCSD, and Univ of Washington. Based on this experience, he launched the CoCalc web application in April 2013, under the name SageMathCloud, with the mission to make it very easy to collaboratively use free open source mathematics and data science software in classes and research.
After over 5 years of extremely active development, CoCalc is now a modern web application that provides collaborative access to most free open source technical software, including LaTeX, Jupyter Notebooks, the Python numerical ecosystem, the R statistics software, and SageMath. Thus CoCalc brings together the work of thousands of contributors to open source software under one roof, which is easily accessible from your web browser.
Hal Snyder • • cocalc and python
NOTE: This blog posting has been updated. See Dash with CoCalc (2021 version) for the updated article.
Create interactive data visualizations for collaborators in your CoCalc projects using Dash.
Dash is an open-source framework to create web applications with Python. With CoCalc’s HTTPWebserver capability, you can run a Dash application from inside a CoCalc project.
Hal Snyder • • cocalc, python, and r
If you are new to coding, CoCalc makes it easy to get started. All you need is a web browser and an Internet connection. You don’t have to install software on your computer to start learning Python, R, Julia, and other leading open-source languages.
Harald Schilly and Hal Snyder • • cocalc
Add scientific computing to any online training platform by embedding CoCalc.
Embedding CoCalc into an online learning platform or learning management system (LMS) adds:
Harald Schilly • • cocalc
CoCalc wants you to fully accomplish your computational work online. To archive this goal, CoCals has to provide a reliable service, offer and maintain the software you need, and package this in a powerful interface.
The new “Assistant” is one of the latest additions to the interface. Its goal is to help you by offering a curated set of annotated code snippets.
